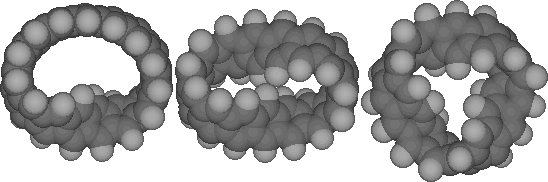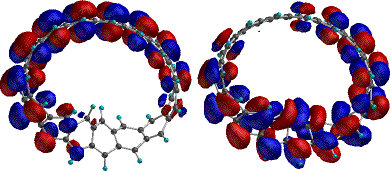Supplementary Material (ESI) for Perkin Transactions. This journal is © the Royal Society of Chemistry
Twist localisation in Single, Double and Triple Twisted
Möbius cyclacenes
Twist localisation in Single, Double and Triple Twisted
Möbius cyclacenes
Sonsoles Martín-Santamaría, and Henry S.
Rzepa*
Department of Chemistry, Imperial College of Science,
Technology and Medicine, London, SW7 2AY, UK
Summary: The AM1 and ab initio calculated
geometries of Möbius strips formed by imparting one, two
or three twists to cyclacenes of various lengths reveal a
localisation of the twist over 2-4 benzo rings.
Various properties of these systems are reported, including the
geometries, the form of the highest occupied molecular
orbitals, the electrostatic potential, and the charge
distributions in neutral, 6+ and 6- forms of these molecules.
Factors influencing the localising tendency are discussed.
There has been a recent revival of interest in Möbius
topologies in aromatic conjugated molecules. Several
suggestions for Möbius-like systems in small and medium
sized rings have been made,1 and a Möbius-like
conformation of [16] annulene has been proposed.2
Türker3 has considered (hypothetical) Möbius systems
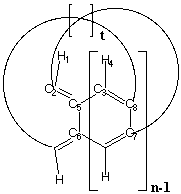
formed from a cyclic acene, or cyclacene (Scheme 1). Here the
focus was on the aromaticity arising from the peripheral
circuit, which in a Möbius system forms a single
continuous edge. The schematic diagram shown of the geometry of
this system,3 appeared to indicate a non uniform
distribution of the twist present in the molecule. We now
report an investigation of this aspect, together with results
for doubly and triply twisted cyclacenes, which have not
hitherto been reported.
Computational Procedure
Initial calculations were performed using the Chem3D (V 5.0)
implementation of the AM1 semi-empirical SCF-MO method. Care
was taken to optimise all geometries to a gradient norm value of less
0.1 for cyclacenes containing either n=8 or n=15 benzenoid
rings for ring twists corresponding to t=1-3 (Scheme 1).
Optimisation to a greater tolerance of 0.01 revealed no
significant difference from the previously optimised values.
Ab initio calculations at the STO-3G level used
G98W4. The Chem3D interface was used to visualize
the 3D form of the molecular orbitals and electrostatic
potential. The 3D rendered orbitals were contoured at 0.005
a.u, saved in 3DMF file format, and compressed for display. To view
these orbital models via the supplemental information version
of this article (available via http://www.rsc.org/suppdata/p2/b0/b005560n) a 3DMF viewer such as the Quick3D browser plugin or 3DMF Optimizer is required, together
with
QuickDraw3D libraries.
Characteristics of Single Möbius Twist
Cyclacenes
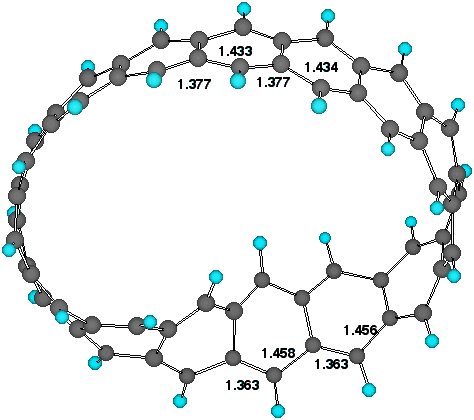
The most conspicuous feature of the singly twisted systems
(n=8, 15, t=1, Table 1) is indeed that the twist is not evenly
distributed around the ring. The degree of regular bond
alternation along the periphery (Figure 1) increases noticeably
in the more highly twisted region. The degree of twist can be
quantified by measuring two types of dihedral angles,
H1-C2-C3-H4 at the periphery and C5-C6-C7-C8 (Scheme 1) at the
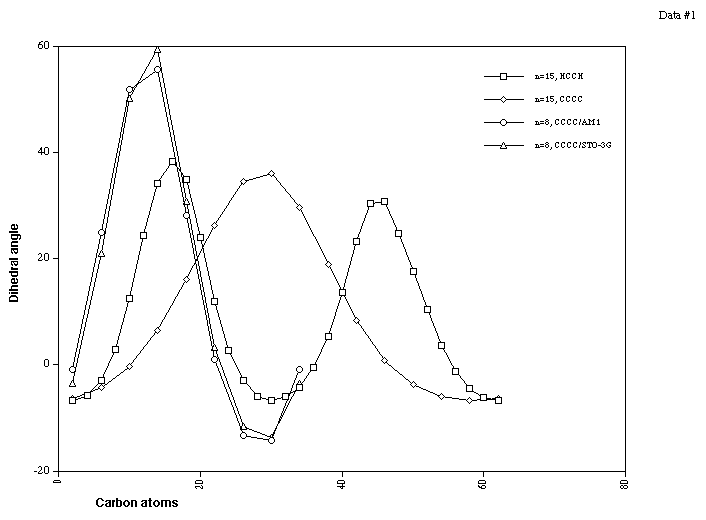
ring junctions. Figure 2 shows the values for both a small
highly strained cyclacene (n=8) and for the larger system n=15,
which has 15 sets of C5-C6-C7-C8 (referred to as CCCC) and 30
sets of H1-C2-C3-H4 (referred to as HCCH) angles. For both
sized rings, several effects merit discussion.
A clear maximum in the adjacent CCCC dihedrals is observed,
indicating a significant degree of localisation of the twist.
Two maxima are observed for the HCCH measurements,
corresponding to two circuits of the ring back to the starting
point, as is of course appropriate for a Möbius ring. We
note particularly that the two maxima in this case are not
equal in value. Inspection of the 3D geometry reveals that
although there is only a single periphery, localisation of the
twist means it has both an inside and an outside edge, each
with different properties. This observation in turn reflects on
another well known property of formal Möbius strips, their
non orientable properties, i.e. the distinction between left-
and right-handedness cannot be preserved consistently over the
whole surface. In a time-independent analysis, the localisation
of the twist means the topology is indeed orientable. We also
note that whilst the maximum value of dihedral angle between
two adjacent benzo rings is approximately 35 degrees, the
minimum value is actually of opposite sign. The difference
between the maximum and minimum values increases as the ring
size decreases. It remains to be established whether this
localisation phenomenon will vanish for an infinitely large
cyclacene.
To evaluate whether the twist localisation was a feature of
the Hamiltonian used, we also re-optimised for n=8 at the ab
initio level using an STO-3G or 3-21G bases, obtaining
essentially identical results compared with AM1 (Figure 2),
implying the localisation may be insensitive to the precise
nature of the potential energy function. Further analysis of
the relationship between the potential function and propensity
towards twist localisation will be reported in a subsequent
article.
Localisation of the twist also impacts upon other computed
properties of the cyclacene surface. The highest occupied
molecular orbital (HOMO) and HOMO-1 (Figure 2) differ in energy
by 0.2 eV, and are both delocalised over approximately 12 of
the 15 benzo rings, but the HOMO (and LUMO) has little density
in the region of twist, whilst the lower energy HOMO-1 shows
complementary behaviour, having larger coefficients in the
region of the twist. The conventional expectation is that
reducing orbital overlap by geometrical distortion will raise
rather than lower the energy of a molecular orbital. This
orbital behaviour are also seen for the ab initio 3G and
3-21G wavefunction. We note here a
recent report5 relating to the dynamics of creation
and annihilation of soliton pairs upon photo excitation of
polyene chains. The analogy with twist and charge localisation in
the Möbius cyclacene system is currently being investigated.
Finally in this section, we note that the computed molecular
electrostatic isopotential (Figure 3) indicates the negative
region of the potential occurs on the inside concave surface of
the aromatic p system.
Characteristics of Neutral Doubly and Triply Twisted
Cyclacenes
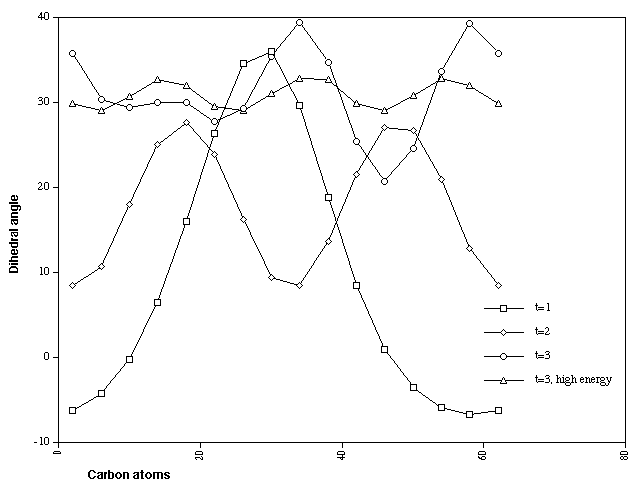
Figure 5 illustrates the calculated CCCC dihedral angles for
single, double and triply twisted Cyclacenes (n=15, t=1-3). As
with the singly twisted system, the double twist shows two
regions of localisation, although the difference between the
maximum and minimum values (~18 degrees) is less than half that
of the singly twisted system. The triply twisted system
unexpectedly resulted in location of two isomers differing in
energy by 28 kcal/mol (Table). The more stable form appears to
show two highly localised twist regions and a smaller less
distinct one. The less stable isomer, which has C3
symmetry, reveals three equally localised twist regions, but
with a small difference (4 degrees) between the maximum and
minimum degree of twist. This form was verified as an energy
minimum by calculating its force constant matrix. These two
isomers also show different patterns of alternating bond
lengths around the ring periphery (Figure 6). Remarkably, the
C3 symmetric form shows regions along the periphery
where almost no bond alternation occurs, and others where
alternation of up to 0.1Å is seen. We are unaware of any
other conjugated system which shows such behaviour.
Characteristics of Charged Twisted Cyclacenes
To probe the factors that might affect the characteristics
of the twist in these systems, we also looked at the properties
of the charged systems, arguing that adding or removing
electrons would remove electrons from bonding
p-p orbitals, or add them to
antibonding orbitals, hence making the backbone more flexible
and potentially influencing the ability of the ring to twist.
The results indicate the single twist localisation is little
changed by changing the electron occupancy by twelve electrons
(Figure 7). The charged double twist systems (Figure 8) show
that the effect of the charge is to increase the difference
between the minimum and maximum twist values, indicating that
making the benzo-ring more flexible does have a small effect on
the localisation. If greater flexibility increases the
localising effect, then more rigidity would be required to
remove it. It is difficult to see how this could be achieved
chemically. Finally in this series we note the charged triple
twist systems (Figure 9) show the localisation phenomenon to be
almost eliminated, this being more true of the negatively
charged system.
Atomic Charge Distribution
Since charge distributions induced by twisting or photoexciting
a polyene are of general interest in several areas of
chemistry5 we inspected the calculated AM1 Mulliken
charges on the periphery. Those on the hydrogen atoms only
(Figure 10) reveal two small maxima associated with the maximum
in the ring twist, that corresponding to the inside facing
hydrogens being the slightly more positive. The hexapositive
system has more prominent features, with the least positive
hydrogens now being clearly located in the region of inside
facing twist, whilst the outside facing hydrogens are the most
positive and are again associated with the region of maximum
twist. The hexanegative system is essentially the mirror image
of the positive system. Here the most positive hydrogens are
inside the ring and localised at the twist. These effects are
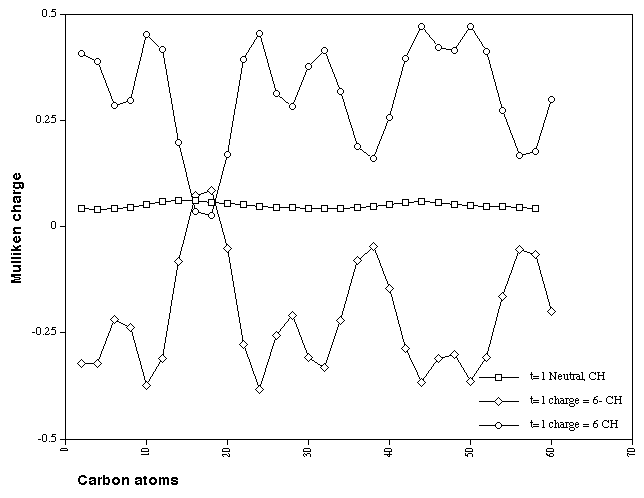
amplified if the charge on the hydrogen and the carbon it is
connected to are summed (Figure 11), as are additional maxima
and minima in the charge distribution.
Conclusions
Whilst the mathematical features of Mobius strips have been
studied since the last century, it is only recently that the
construction of such topologies from flat molecular aromatic
strips has attracted chemists' attention. The use of cyclacenes
as a suitable model for quantitative modelling using molecular
orbital Hamiltonians to describe their behaviour has revealed
an interesting localisation phenomenon of the twist. Two
features of these systems remain to be clarified. Firstly, is
their localising behaviour essentially a chemical phenomenon,
or does it have deeper topological meaning? Secondly, a
molecular dynamics treatment will be required to understand their
time-dependent properties, together with associated
properties such as whether a rotating charge distribution in such a
cyclacene can be induced, and e.g. its behaviour in a magnetic field.
Acknowlegements
We thank P. v. R. Schleyer (Erlangen) and I. Stewart (Warwick)
for stimulating discussions.
Table 1 Calculated Energies for Cyclacenes
a Ab initio RHF/STO-3G basis
b
Ab initio RHF/STO-321 basis
Figures
Figure 1. Twist localisation and adjacent bond lengths (AM1)
for Cyclacene, n=15, t=1.
Figure 2. HCCH and CCCC Dihedral angles for Cycloacenes, n=15,
t=1 and n=8, t=1.
Figure 3. (a) AM1
HOMO (-6.73ev) and (b) HOMO-1 (-6.93eV) for Cyclacene, n=15,
t=1.
Figure 4. AM1 Computed Molecular
Electrostatic Potential for Cyclacene, n=15, t=1.
Figure 5. CCCC Dihedral angles for Cyclacene, n=15, t=1-3.
Figure 6. Peripheral C-C bond lengths Cyclacene, n=15, t=3 for
(a) low energy form (b) high energy form.
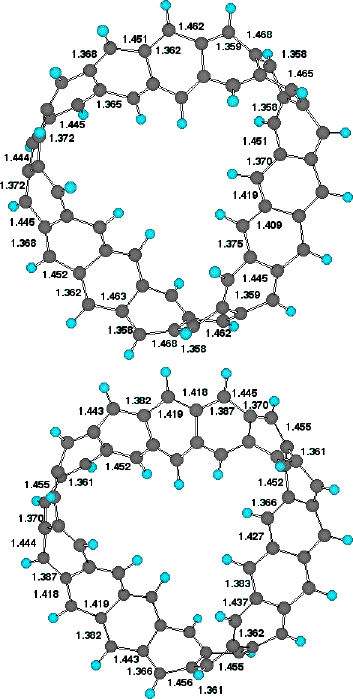
Figure 7. HCCH Dihedral angles for Cyclacene, n=15, t=1, with
charge 0, +6 and -6.
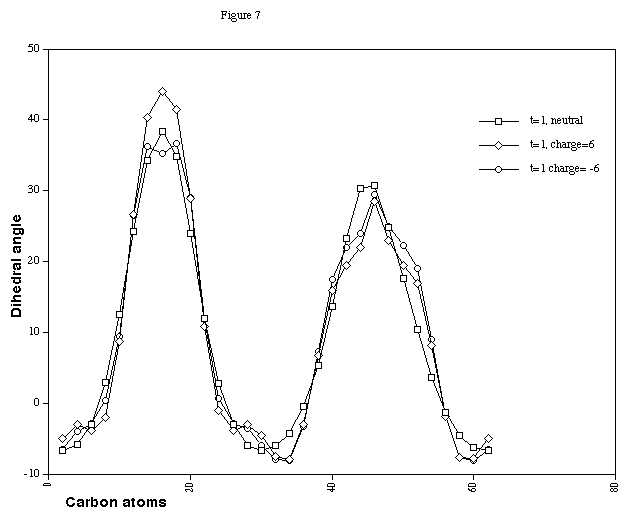
Figure 8. CCCC Dihedral angles for Cyclacene, n=15, t=2, with
charge 0, +6 and -6.
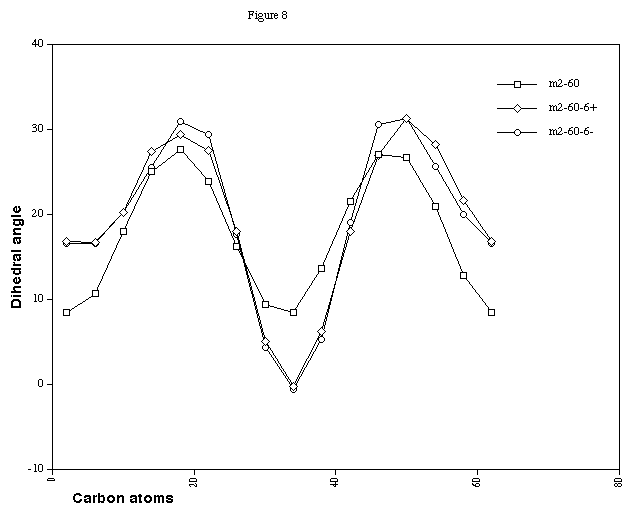
Figure 9. CCCC Dihedral angles for Cyclacene, n=15, t=3, with
charge 0, +6 and -6.

Figure 10. Calculated Mulliken charge distributions on the H
atoms for Cyclacene, n=15, t=1, with charge 0, +6 and -6.
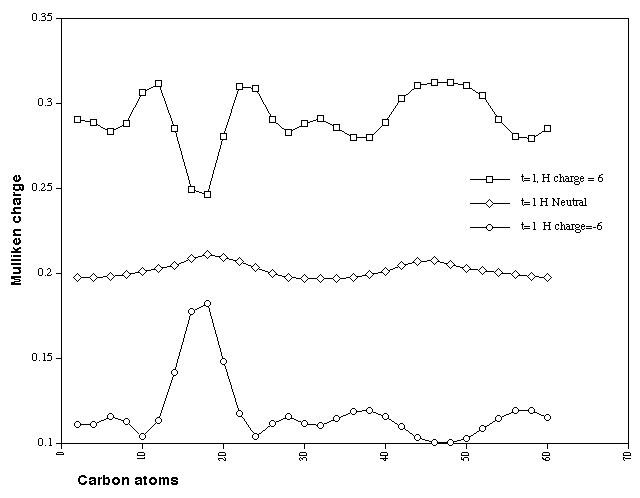
Figure 11. Calculated Mulliken charge distributions on the
combined HC atoms for Cyclacene, n=15, t=1, with charge 0, +6
and -6.
- E. Heilbronner, Tetrahedron Lett., 1964,
29, 1923; M. Mauksch, V. Gogonea, H. Jiao and P. v. R.
Schleyer, Angew. Chem., Int. Edition, 1998,
37, 2395
- S. Martin-Santamaria, B. Lavan and H. S. Rzepa,
Perkin Trans. 2, 2000, 1415; M. Mauksch, Thesis,
Erlangen 1999 (P. v. R. Schleyer and M. Mauksch, personal
communications).
- L. Turker, J. Mol. Struct. (Theochem), 1998,
454, 83.
- Gaussian 98, M. J. Frisch, G. W. Trucks, H. B. Schlegel,
G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G.
Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant,
S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C.
Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi,
B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski,
G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K.
Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J.
Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A.
Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L.
Martin, D. J. Fox, , T. Keith, M. A. Al-Laham, C. Y. Peng, A.
Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B.
G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M.
Head-Gordon, E. S. Replogle, and J. A. Pople, Gaussian, Inc.,
Pittsburgh, PA, 1998.
- M. Garavelli, B. R. Smith, M. J. Bearpark, F. Bernardi,
M. Olivucci and M. A. Robb, J. Am. Chem. Soc.,
2000, 122, 5568; W. R. Salaneck, R. H. Friend and J. L.
Bredas, Phys. Rep., 1999, 319,
232; I. G. Hill, A. Kahn, J. Cornil, D. A. dos Santos and J. L. Bredas,
Chem. Phys. Lett., 2000, 317, 444.