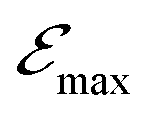Additions and corrections

Assistance of metal nanoparticles in photocatalysis – nothing more than a classical heat source

Y. Sivan*, I. W. Un and Y. Dubi

Faraday Discuss., 2019, 214, 215–233. Amendment published 09 April 2020.

The authors regret that the definition of R on page 220 is incorrect in the original article. The correct definition, in which 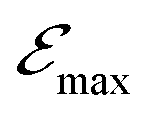is replaced with ℏω_p, is given below:

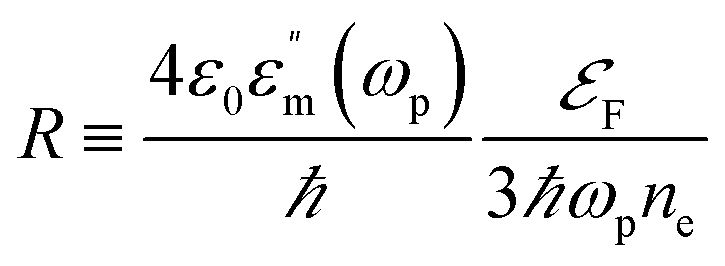
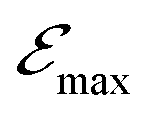has also been replaced by ℏω_p in a number of places in Appendix A and any corresponding calculated values have been updated. The equations affected are equation A7, the equations for R and 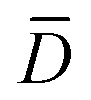, and the value of Δf. The second row of Table 1 has also been updated to define ω_p. The full corrected appendix is shown below.

Additionally, the equation in the second last paragraph of page 226 in the original article is incorrect. The corrected version is shown below and in the corrected Appendix A reproduced below.

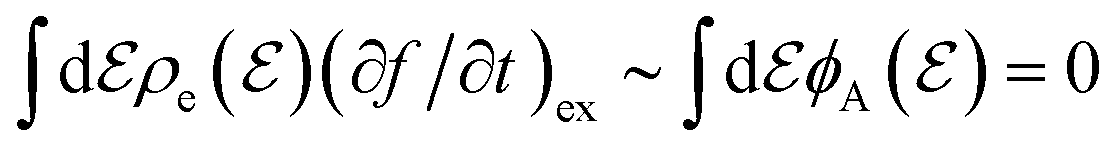
In addition, the characters 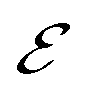, , 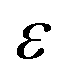and E, were use incorrectly in Appendix A in the original article and are updated here for clarity.

Appendix A. An estimate of the quantum mechanical excitation term for CW illumination of a metal nanoparticle

We employ the elegant expression proposed in ref. 57; namely, we define 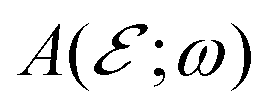such that 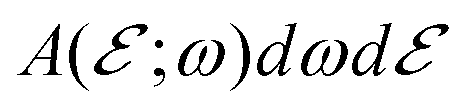is the (joint) probability of photon absorption of frequency between ω and ω+dω for the final energy 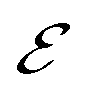measured with respect to the bottom of the band at 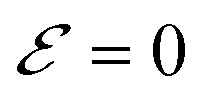. We define this probability as

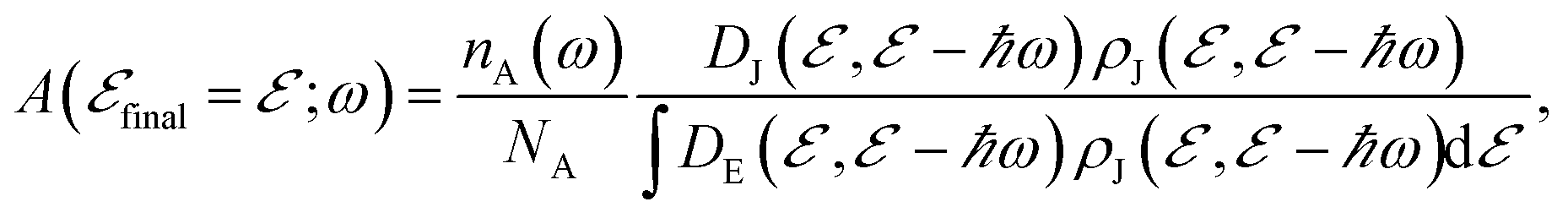
(A1)

where 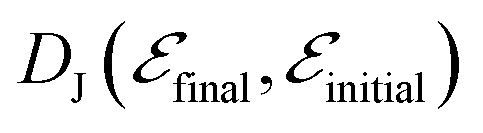is the squared magnitude of a transition matrix element for the electronic process 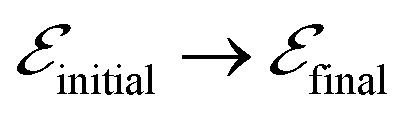. Furthermore, ρ_J corresponds to the population-weighted density of pair states,

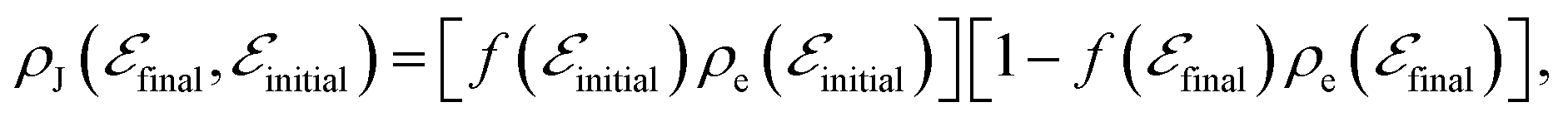
(A2)

and 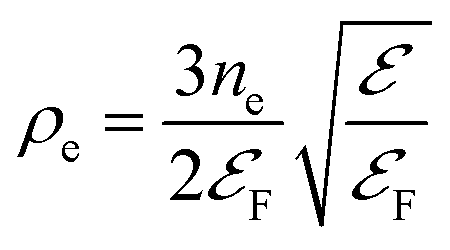is the density of states of a free electron gas;⁵⁰ n_e is the electron density. Finally, n_A(ω) is the number density of absorbed ℏω photons per unit time between ω and ω+dω, and 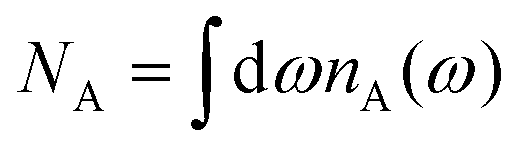is the total number density of absorbed photons per unit time. For CW illumination, this is given by

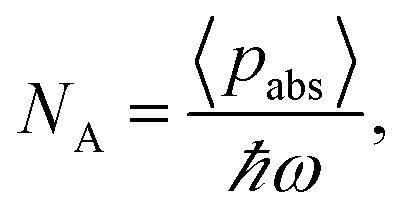
(A3)

where the averaged absorbed optical power density (in units of W m⁻³) is given by the Poynting vector,⁸⁶ namely

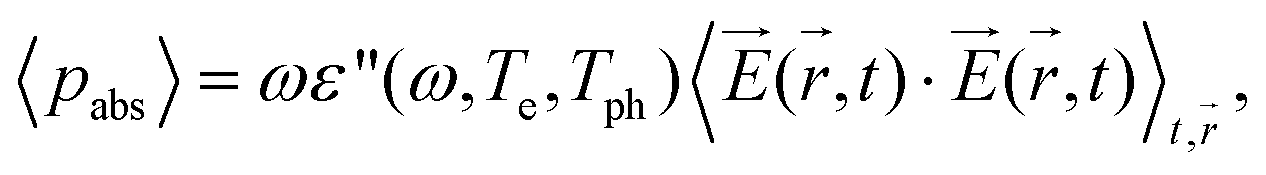
(A4)

where 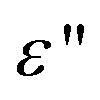is the imaginary part of the metal permittivity, and the spatio-temporal averaging, 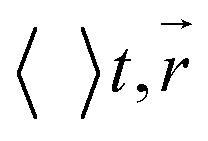, is performed over a single optical cycle such that only the time-independent component remains and is over the NP volume.

The net change of electronic population at energy 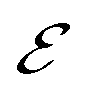per unit time and energy at time t due to absorption is 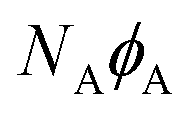, where

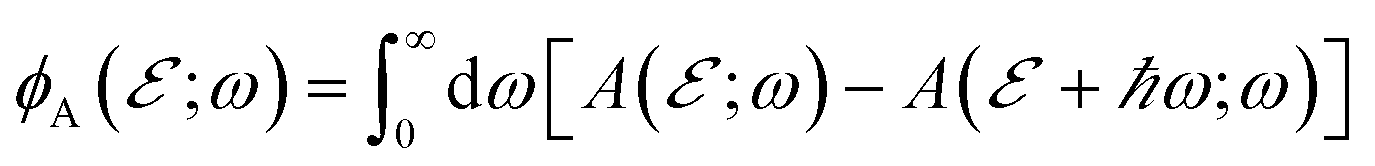
(A5)

describes the total (probability of a) population change at energy 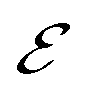per unit time and energy at time t. Altogether,

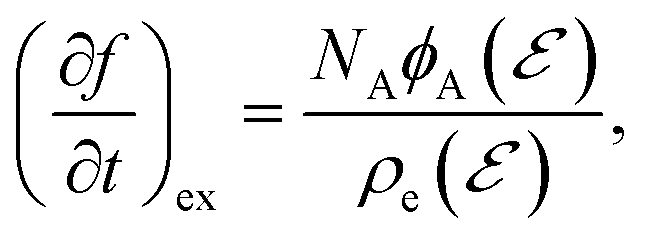
(A6)

meaning that electron number conservation is ensured, .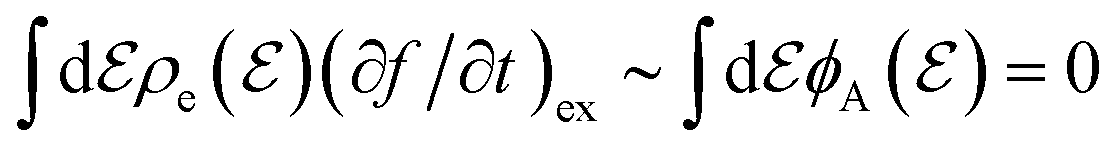

For CW illumination, 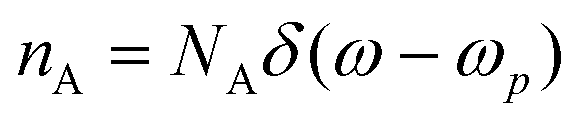and 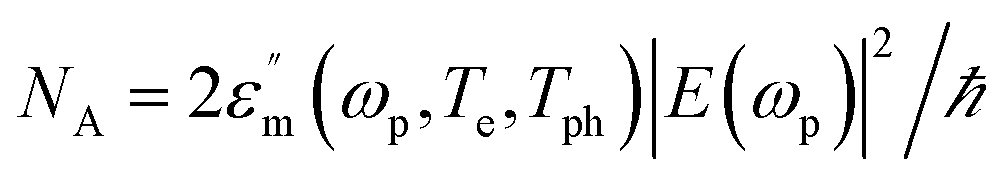. For the low intensities considered here, one can ignore the temperature dependence of the metal permittivity.^38,87

For simplicity, we now approximate ρ_e by its value at 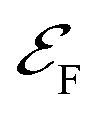. In the same spirit, we define the normalized transition matrix element 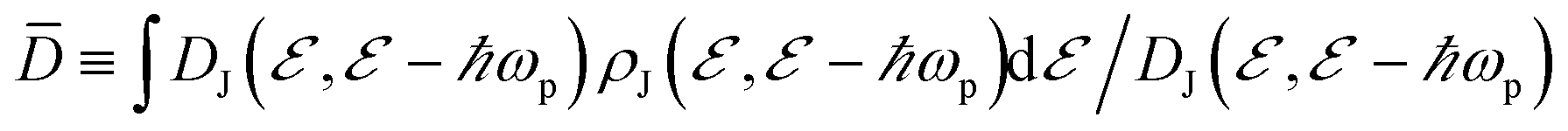and ignore its energy-dependence. Thus, we also find that 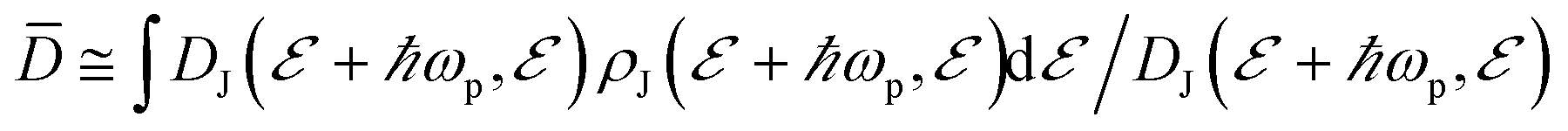, meaning that 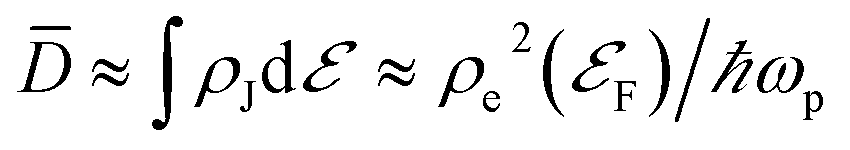. In this case, the excitation rate (A6) can be approximated by

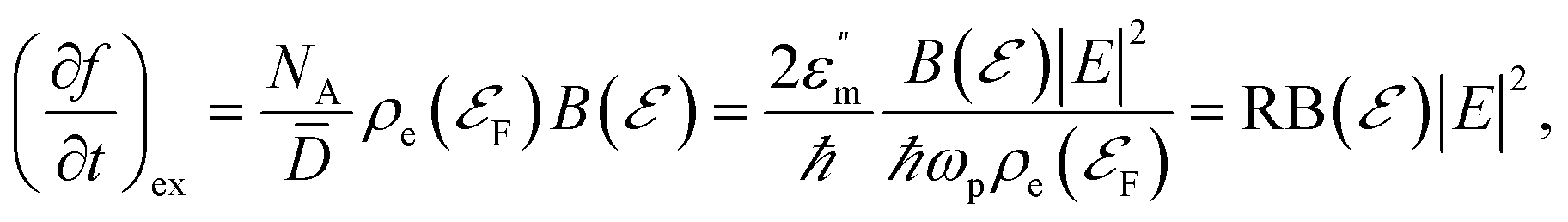
(A7)

where 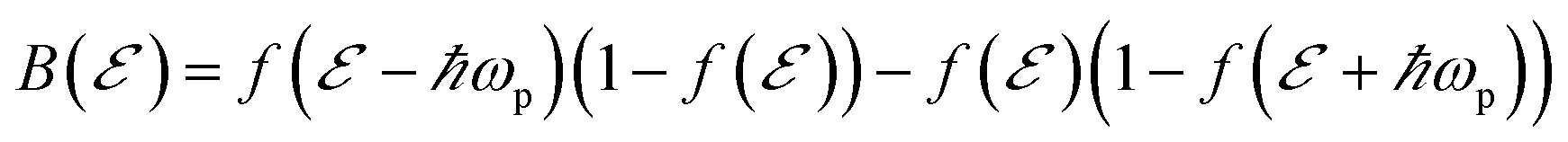is a dimensionless O(1) function representing the 2ℏω_p step-like energy dependence of the quantum excitation term and 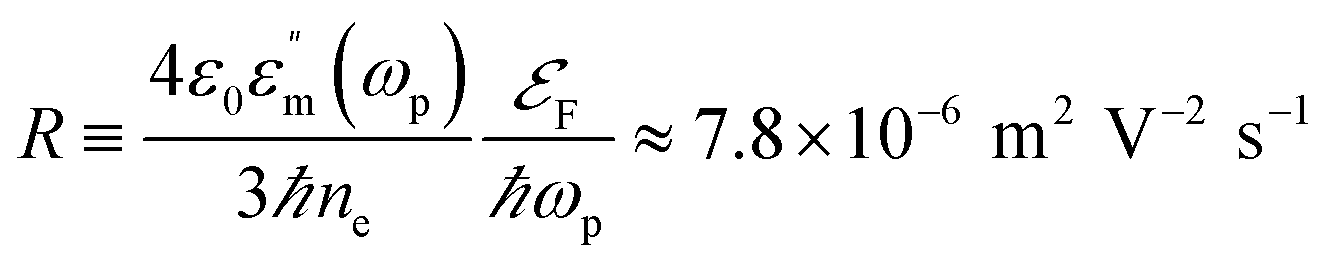(see the parameter definitions and values in Table 1). Thus, we can estimate the non-thermal carrier density as

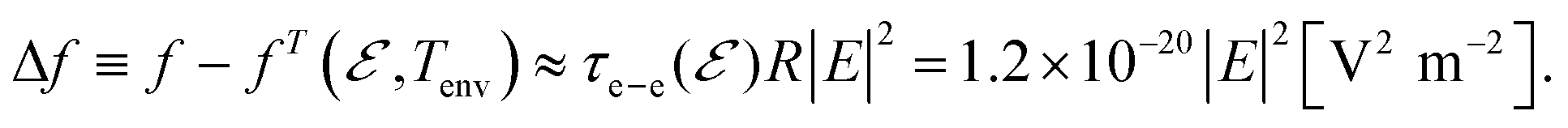
(A8)

Table 1 Parameters used in the simulations and the values chosen for (low quality)⁷³ Ag

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

Back to article