Additions and corrections

Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature

Reinhard Lipowsky^a

Faraday Discuss., 2013, 161, 305–331 (DOI: 10.1039/c2fd20105d). Amendment published 17th October 2013.

In section 6 of Ref.¹, lipid vesicles enclosing two aqueous phases, α and β, have been considered. These phases typically form two droplets that partially wet the vesicle membrane and, thus, partition this membrane into two distinct membrane segments, αγ and βγ, with surface areas A_αγ and A_βγ. In Section 6.1, it was argued that the vesicle shapes involve only a single Lagrange multiplier tension, Σ, which is conjugate to the total membrane area A = A_αγ+A_βγ, because we have only a single constraint acting on this total area. The latter argument is, however, deceptive: in general, we need two Lagrange multiplier tensions Σ_αγ and Σ_βγ as one can see most clearly if one views these two quantities as the mechanical tensions that act to stretch (or compress) the two membrane segments.

Thus, consider the equilibrium shapes of vesicles with minimal energy E_ve for fixed droplet volumes V_α and V_β as a function of total membrane area A. For each value of A, these equilibrium shapes are characterized by certain segmental areas A_αγ and A_βγ. Likewise, the bending energy of these shapes consists of two terms, E_be,αγ(A_αγ) and E_be,βγ(A_βγ), corresponding to the two segments. The mechanical tensions Σ_αγ and Σ_βγ within these segments are then given by

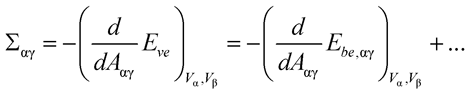(1)

and

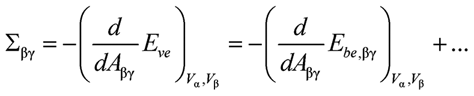(2)

where the derivatives are taken at constant volumes V_α and V_β. The dots indicate terms arising from additional energy contributions² of the αβ interface and the contact line. The values for Σ_αγ and Σ_βγ as obtained from (1) and (2) will, in general, differ because the two membrane segments are exposed to different environments and are, thus, characterized by different elastic parameters. In addition, the segmental areas A_αγ and A_βγ can depend on the total membrane area A in a nonlinear manner, reflecting the variable partitioning of this area between the two segments.

For Σ_αγ ≠ Σ_βγ, the equations (66) and (67) in Ref.¹, which describe the total membrane tensions 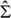_αγ and 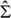_βγ, assume the form³

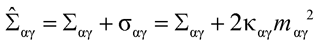(66*)

and

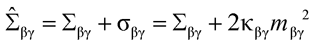(67*)

Furthermore, the relation (73) in Ref.¹ is then replaced by

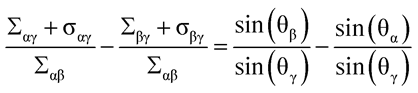(73*)

and the equations (77) - (79) are no longer valid. Finally, equation (80) in Ref.¹ now attains the more general form

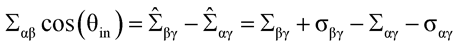(80*)

If the αγ membrane segment forms nanotubes, the mechanical tension Σ_αγ of this segment can be neglected because it is much smaller than the spontaneous tension σ_αγ,¹ and the total tension

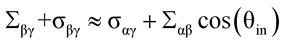(3)

within the βγ segment must balance both the spontaneous tension σ_αγ of the αγ segment and the interfacial tension Σ_αβ of the liquid-liquid interface between the two droplets.

References

1 R. Lipowsky, Faraday Discuss., 2013, 161, 305–331.

2 H. Kusumaatmaja, Y. Li, R. Dimova and R. Lipowsky, Phys. Rev. Lett., 2009, 103, 238103.

3 Y. Li, R. Lipowsky and R. Dimova, Proc. Nat. Acad, Sci. USA, 2011, 108, 4731–4736.

^a Theory and Bio-Systems, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam, Germany;Fax: +49 331 567 9602; Tel: +49 331 567 9600; E-mail: lipowsky@mpikg.mpg.de