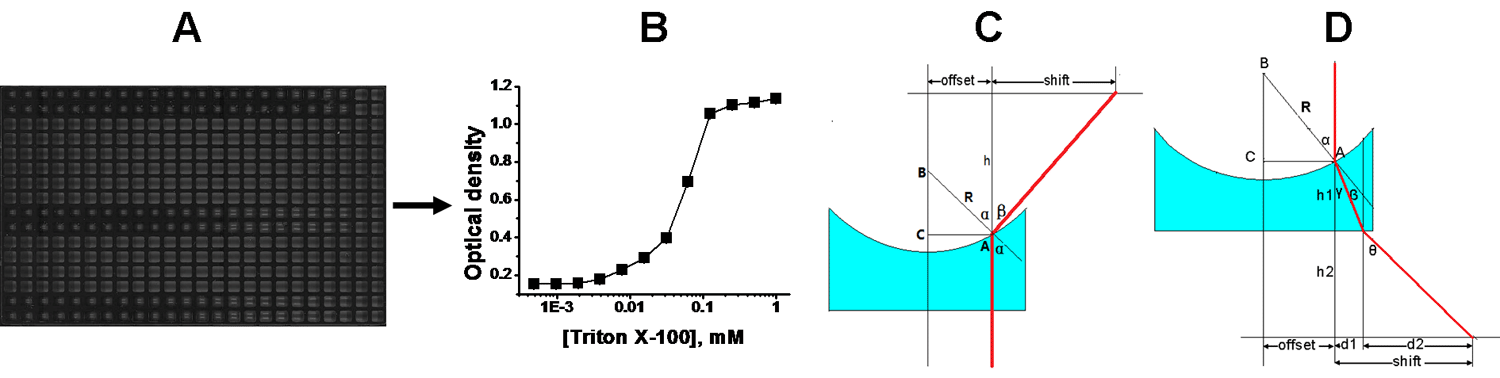
Fig. 1 Converting liquid surface curvature variations in microplate wells into quantitative absorbance signals. (A) Various liquid surface curvatures are formed in microplate wells for solutions with different surface tensions by the capillary effect. Photograph of a Greiner 384-well black/clear microplate, two rows of wells at top, middle and bottom contain 30 ml Triton X-100 solution in serial dilution, the last two wells in each row contained buffer only; the remaining rows are empty. The liquid surface curvature variations are distinguishable by eye from their different reflection of light. (B) Absorbance signal vs. Triton X-100 concentration in the microplate wells measured using a Molecular Device SpectraMax M5 plate reader by offset of the detecting light beam 1 mm from the well center and detected at 900 nm wavelength. (C) Light paths in the instrument for absorbance measurement in a top-read instrument (Molecular Device SpectraMax M5 plate reader used in this manuscript). (D) Light path for bottom-read instrument. The light beam was offset from the well center to enable refraction from a different normal at different liquid surface curvature. The vertical detecting light beam (red line) passes through the liquid (azure shadow)–air interfaces with refraction and reaches the detector with a shift from the original vertical location. The shift value can be calculated by solving the triangles with known h1 and h2 or h, offset, and the refractive index of liquid and air, n2, n1, at a given liquid surface curvature radius R (for detail see Supplementary Material 3, ESI).
The original Supplementary Materials 3 provides equations for calculation of shift values for a bottom-read plate reader (corrected Fig 1D). In a top-read plate reader, the refracting detecting light beam changes direction only once when leaving the liquid (corrected Fig 1C); like h1, h in the corrected Fig 1C is insensitive to the liquid curvature change when the offset is ~0.7 of the well radius and can be considered as constant for the same liquid volume; based on the same principle, the shift value in Fig 1C can be calculated by the following equations:
Sin(α) = offset/R;
Sin(α+β)/Sin(α) = n2/n1;
Shift = h*tan(β)
Acknowledgement: The authors thank Dr Søren Møller Nielsen, Principal Scientist, Molecular Pharmacology, H. Lundbeck A/S, Ottiliavej 9, DK-2500 Copenhagen Valby, Denmark for identifying this inconsistency.