Additions and corrections
Studying soft matter with “soft” potentials: fast lattice
Qiang Wang
Soft Matter, 2009, 5, 4564–4567 (DOI: 10.1039/b909078a). Amendment published 25th June 2010.
A few mistakes in the lattice self-consistent field (LSCF) calculations in
our original paper need to be corrected. First, the initial condition for the
one-end-integrated propagator qs(r)
in eqn (6) there should be qs=1(r)
= exp[−ω(r)/N]. Due to
the boundary conditions for impenetrable walls (i.e., qs(x = 0) = qs(x
= Lx + 1) = 0 for all s)
used in the paper, this slightly changes the LSCF results of the segmental
density profile fLSCF(x),
non-bonded interaction energy per chain 
(which should be about 0.08466)
and thus 〈npair/nC〉LSCF; the
differences can hardly be seen in Fig. 1 and 2. Similarly, the initial
condition for the propagator Qp,s(x|x′) should be Qp,s=0(x|x′)
= δx,x′
exp[−ω(x)/N].
Second, the mean-square chain radius of gyration in the x direction should be computed as
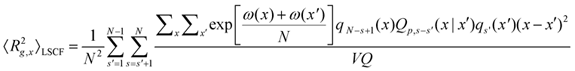
where the term in the summation with s′ = 1 and s = N
is the mean-square chain end-to-end distance in the x direction, 
. While the
formula in the paper gives correct 
, 
reported there is incorrect and should be about
2.2384.
Finally, while our system is homogeneous in the directions parallel to the
confining walls, the LSCF results of chain dimensions in these directions are
not the same as those of random walk in the bulk, i.e., 
and 
for i = y
and z. With the simple cubic lattice model used in the paper, this can
be understood by the fact that, for segments in the lattice layers closest to a
wall (i.e., at x = 1 and Lx), the probability
for the next step of the (confined) random walk being along the y (or z)
direction is 2/5, larger than the value of 1/3 in the bulk. Taking into account
that fLSCF(x
= 1) = fLSCF(x
= Lx) ≈ 0.92647, this gives 
and 
for i = y
and z.
Fig. 3 should therefore be replaced by the figure below, showing that, at
large chain number density C ≳ 0.02, the differences between
our fast lattice Monte Carlo (FLMC) and LSCF results in 
, 
(i
= x,y,z), 
(i
= x,y,z), and f(x)
all scale with 1/C.
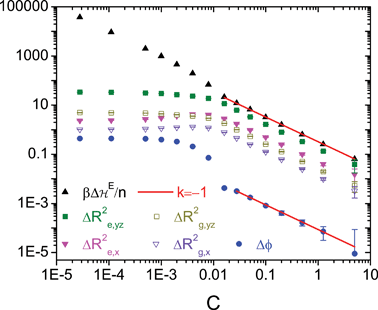
The differences between FLMC and LSCF results in various quantities as a
function of chain number density C, where 
, 
with 
similarly defined, 
with 
similarly
defined, 
and the two straight lines have a slope of –1. Note
that the error bar for 
is smaller than the symbol size and thus not
shown. See the original paper for more details.
The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.
Back to article